Machines in the Media
Questions
Started in the 18th century in Great Britain, the industrial mechanization saw a dramatic acceleration in the 19th century. English, as exptected, reflects these changes at different linguistic levels, particularly in the lexicon, because of the unprecedented speed with which technological innovations took place.- Given large enough datasets, is it possible to automatically detect changes in the meaning of words associated with this process?
- Would the changes detected reflect what the traditional scholarship on the subject (e.g. Görlach 1999, Kay & Allan 2015, Kytö et al. 2006) say on the matter?
Challenge
One of the main reasons why Big Historical Data need specific tools compared to Big Data in general is mainly that, more often than not, historical data is messy, full of orthographic variation, and, most often than not, comes from OCR'd material (i.e. it is full of OCR errors). This makes training good-quality language models trained on it very challenging. Together with the granularity-speed trade-off needed during preprocessing (common to Big Data in general), we thus also need extra steps to make sure that OCR errors are dealt with and that they figure in any evaluation framework we might choose to adopt when training embeddings from them. Compared to smaller historical text collections, Big Historical Data and Big Data in general, because of their mere size, will typically undergo minimal preprocessing, since NLP tasks such as lemmatization, PoS tagging, morphological analysis or dependency annotation (used as 'preprocessing' steps in embedding architectures such as Al-Ghezi & Kurimo 2020 and Levy & Goldberg 2014) may be computationally unfeasible unless we subsample our corpus beyond the temporal variable. In fact, even minimal preprocessing may not be feasible by sticking only to one specific popular library (e.g. spaCy): instead, each preprocessing step will need to be optimized for computational costs by combining specific pipelines from different external libraries, as well as bespoke methods.Data
Digitized 19th-century newspaper collection comprising a total of ca. 4.5 billion tokens, spanning the period 1800-1920. Around half of the tokens come from the Heritage Made Digital digitization project and can be downloaded here. The other half were specially digitized within the Living with Machines project, but are not publicly available yet.(Pre-)processing
The corpus was divided into bins of 10 years each, to obtain models each representing one decade in the 19th century. Each bin was preprocessed by lowercasing the text, removing punctuation and any word with less than 2 characters.Training
The embeddings were trained using Word2Vec (Mikolov et al. 2013) as implemented in Gensim (Řehůřek & Sojka 2010). After a grid-search for the most important parameters, the final models were trained using the following:- sg: 1 (i.e. SkipGram rather than Continuous Bag-of-Words)
- epochs: 5
- vector_size: 200
- window: 3
- min_count: 1
Alignment
In order for the semantic spaces to be comparable, the models were aligned using Orthogonal Procrustes (Schönemann 1966) (i.e. obtaining diachrnonic embeddings). The most recent decade (1910s) was kept fixed, with all other decades aligned to it.Change point detection
Given a word (o set thereof), first calculate the cosine similarity between the vector of the same word in the most recent time slice (in this case the 1910s) and the vector of the same word in each of the previous time slices. Then structure the resulting list of cosine similarity scores in a dataframe like the following:timeslice traffic train coach wheel fellow railway match 1800s 0.42065081000328100 0.3247864842414860 0.48939988017082200 0.40280336141586300 0.4793526530265810 0.45957744121551500 0.5546759963035580 1810s 0.44998985528945900 0.37257763743400600 0.4604988396167760 0.4593697786331180 0.5891557335853580 0.47077488899231000 0.527800440788269 1820s 0.4821169972419740 0.3287739157676700 0.4415084719657900 0.5199856162071230 0.5828660130500790 0.414533793926239 0.5771894454956060 1830s 0.5448930859565740 0.5837113261222840 0.6515539884567260 0.634568989276886 0.6111024618148800 0.5849509239196780 0.5492534637451170 1840s 0.6072453856468200 0.7486659288406370 0.6239444613456730 0.6725128889083860 0.623650848865509 0.5770826935768130 0.5812575817108150 1850s 0.6091518402099610 0.7796339988708500 0.5971360206604000 0.4985277056694030 0.6289939284324650 0.6734532713890080 0.5770257711410520 1860s 0.6446579694747930 0.7618392705917360 0.603736162185669 0.5436286926269530 0.6926408410072330 0.609641432762146 0.6728477478027340 1870s 0.7729555368423460 0.8115466833114620 0.6379809379577640 0.652446448802948 0.7293833494186400 0.7228521108627320 0.6857554316520690 1880s 0.7656214237213140 0.8313593864440920 0.6118263006210330 0.5638831257820130 0.7863538861274720 0.7955769300460820 0.757251501083374 1890s 0.8245968818664550 0.8599095344543460 0.6886460185050960 0.7133383750915530 0.8441230058670040 0.8329502940177920 0.8200661540031430 1900s 0.8344136476516720 0.854633092880249 0.7280615568161010 0.7398968935012820 0.8377308249473570 0.8479636907577520 0.9051868915557860 1910s 1.0 1.0 1.0 1.0 1.0 1.0 1.0 Obviously the cosine similarity between the vector of a word in a decade and itself is equal to 1, which is what we see for the whole of the last row. You can then detect potentially significative change points in each of the columns, that is, an abrupt change in the semantic trajectory of a word. We can apply the PELT algorithm, as implemented in the ruptures library. The algorithm returns timeslices where a changepoint is detected (if any). A change point, for instance, was detected for train and traffic, in the 1820s and in the 1860s, respectively. We can visualize these to make it more intuitive (changepoint is the vertical line):
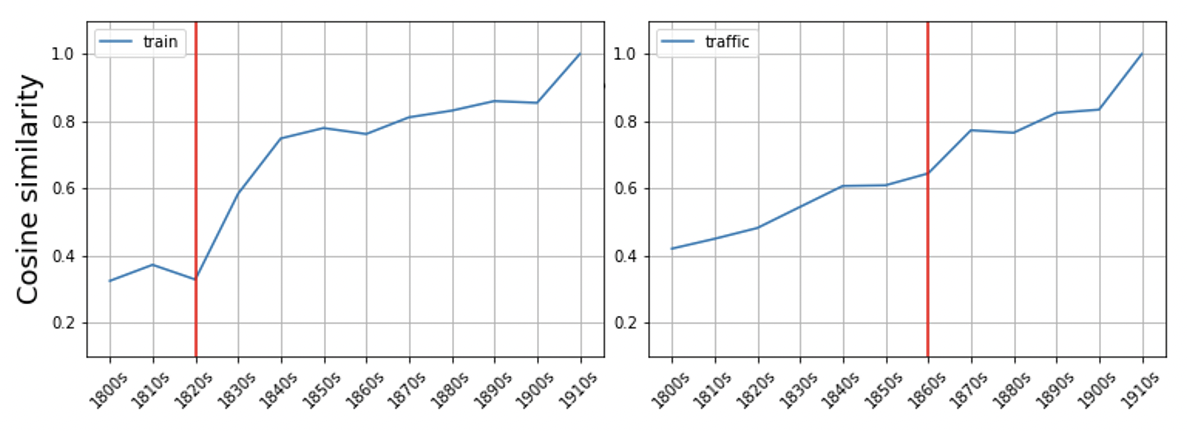
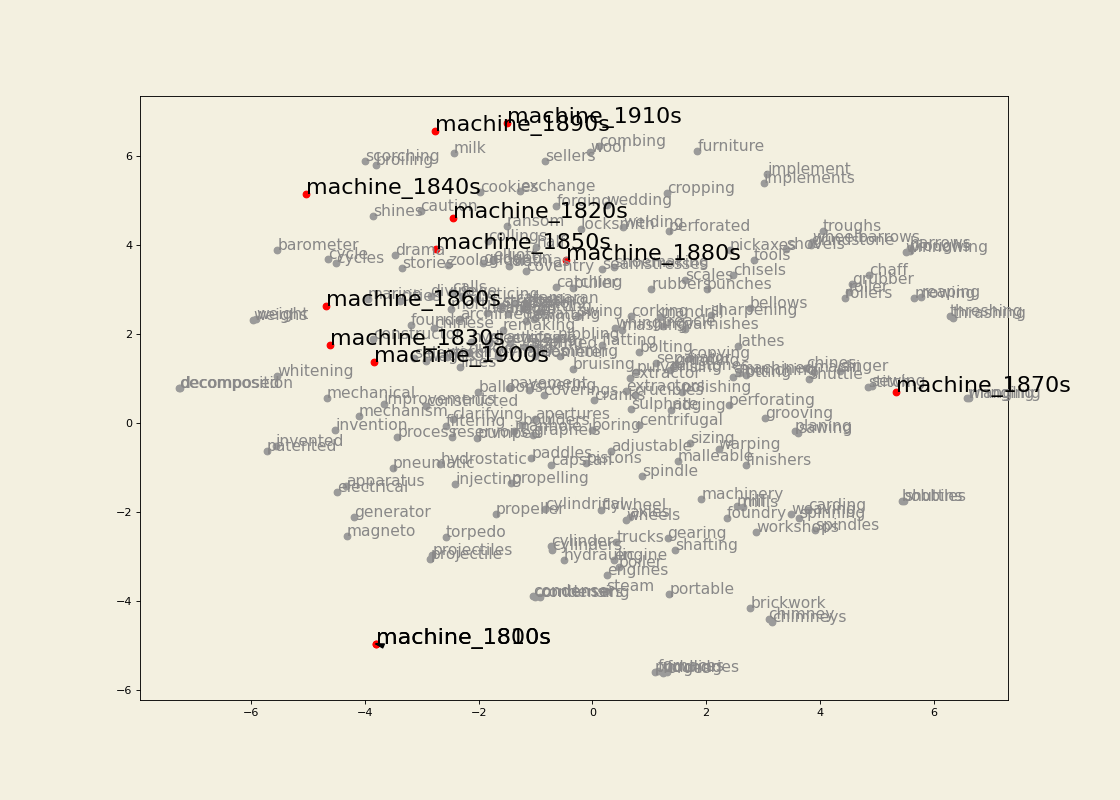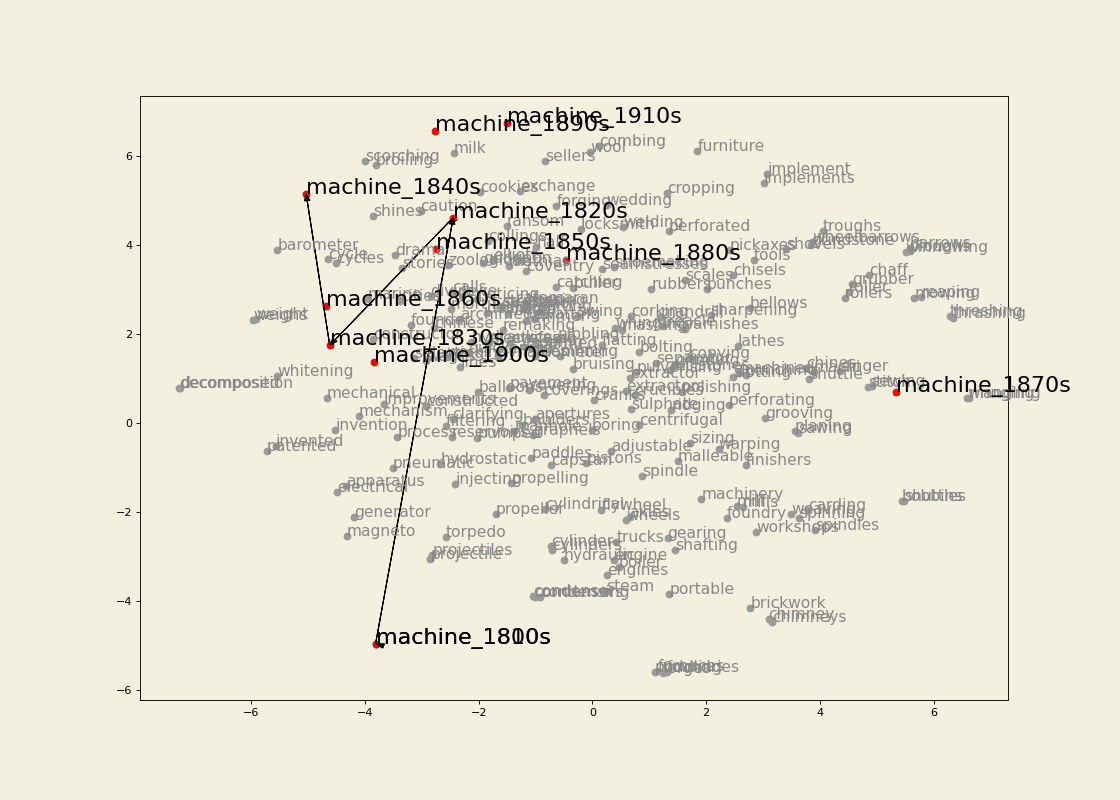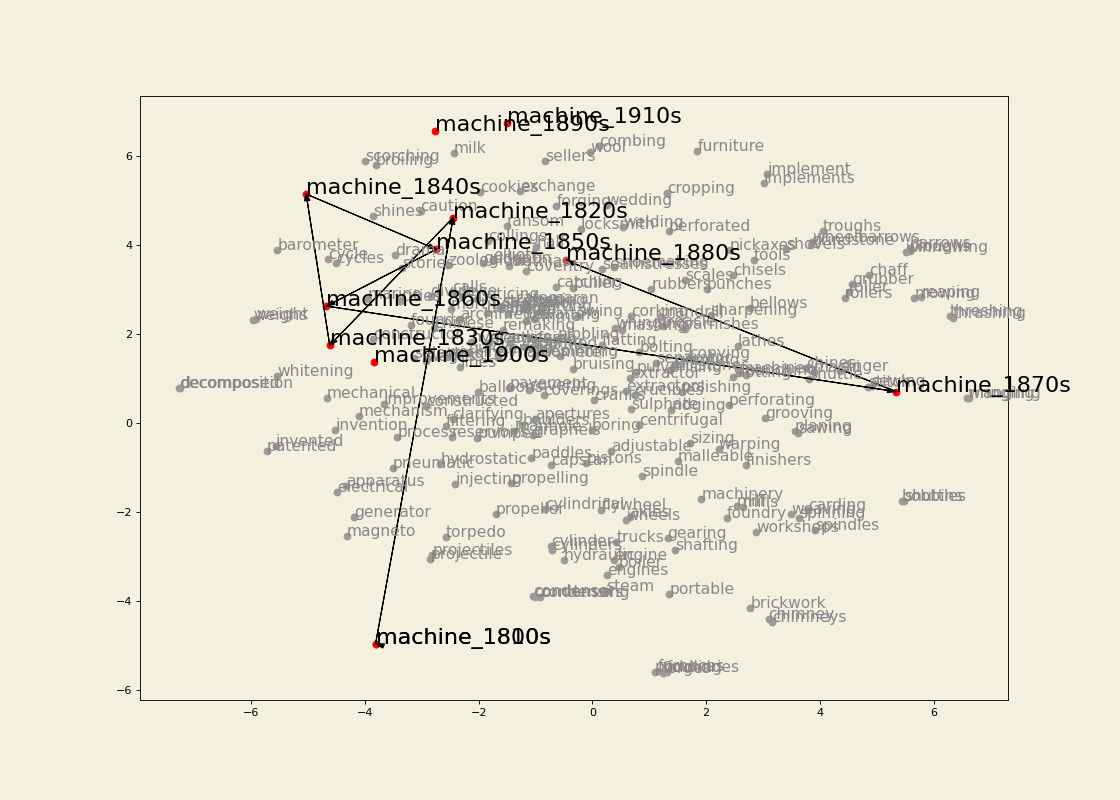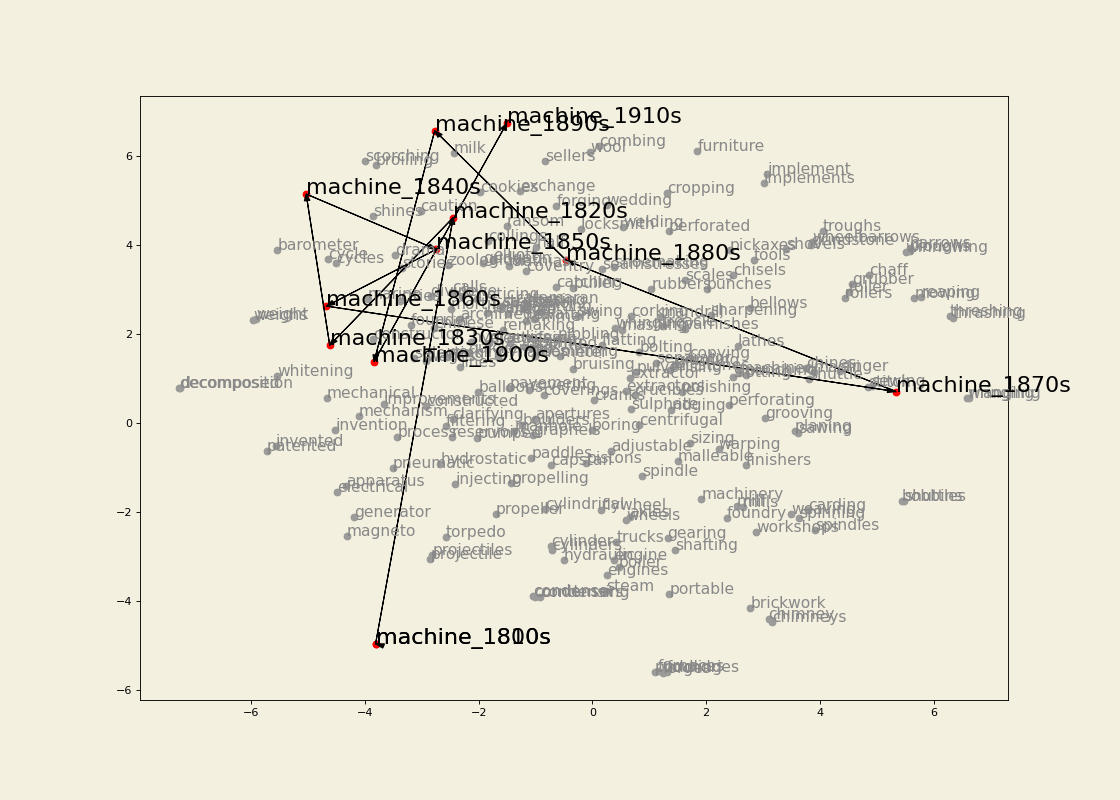
Semantic trajectory visualization
Leveraging the information gathered from the change point detection method, we can also extract the k-nearest neighbours of a word for which a change point has been detected in the decades surrounding the change point and visualize its semantic trajectory to see how the set of most similar words have changed over time. For example, we can extract 30 neighbours for three or four decades for train and traffic. We then keep only the neighbours that are present in the vocabulary of the model for the most recent decade being visualized. Before doing so, however, we make sure that the word vectors corresponding to OCR errors are gotten rid of (I use the pyspellchecker package to identify these), or averaged with the vector for the word with the correct spelling. To the list of vectors being visualized we also add the ones for the word itself (train or traffic) for each of the decade being represented. We then apply TSNE as a dimensionality reduction technique so that we can visualize the vectors in a two-dimensional space. We highlight the relevant words and join them for clarity. The result is the following:
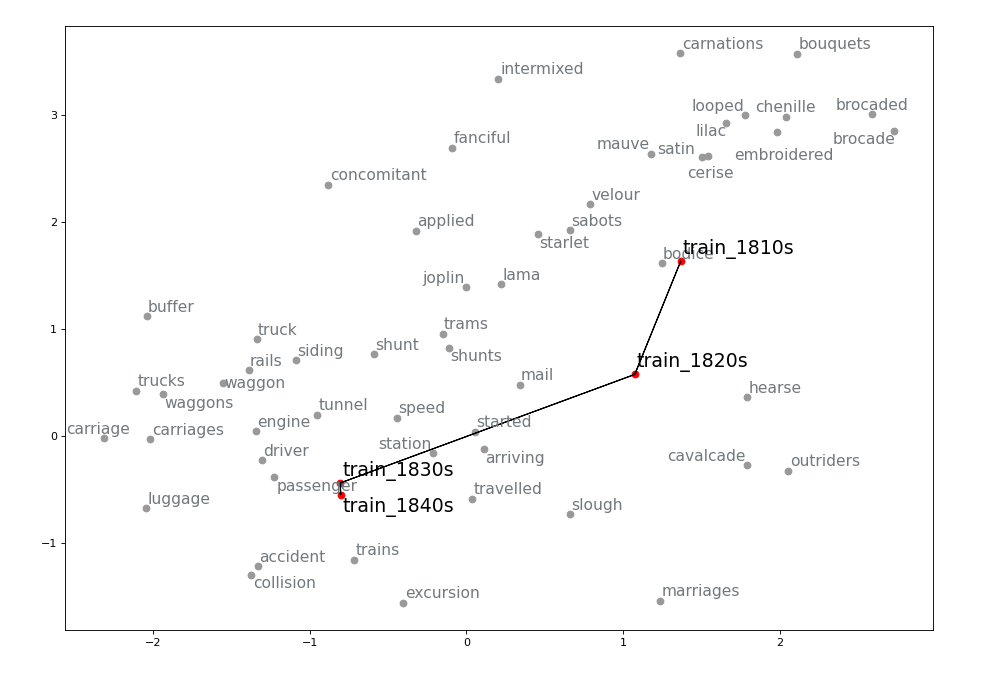
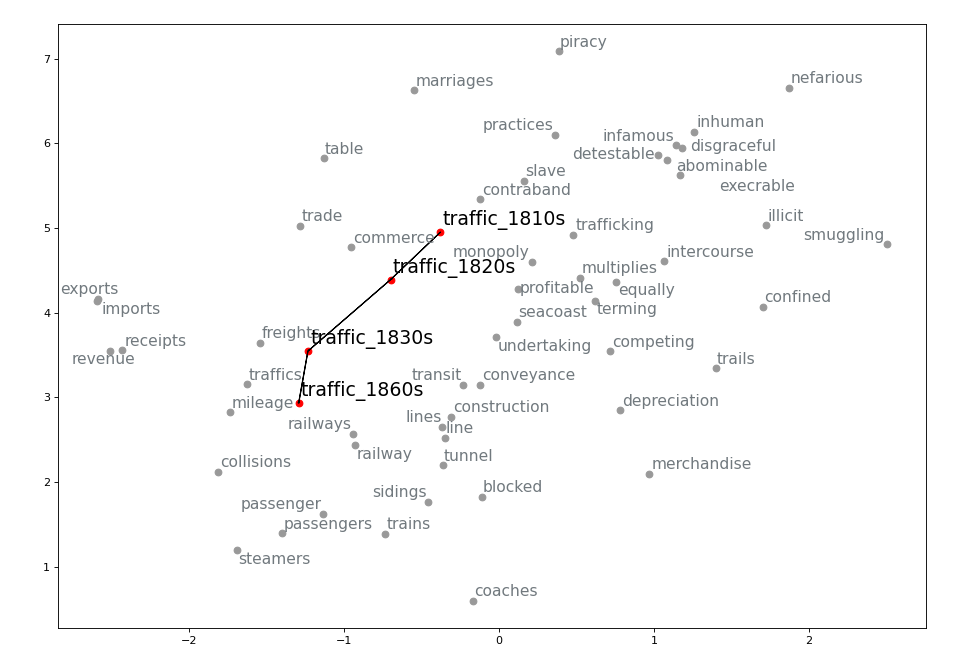
Evaluation
The results from change point detecetion were compared to the semantic changes indicated by the traditional literature, showing that, in fact, our diachronic models largely reflected what claimed there. Change point detection suggests that, given their good-quality and the positive confirmation from the scholarship, diachronic models as the ones described can be used to explore new research questions not yet asked by the traditional literature.Credits
This is a project carried out within Living with Machines (The Alan Turing Institute).
Check out Pedrazzini & McGillivray (2022) for the full case study.References
M. Görlach. 1999. English in Nineteenth-Century England: An Introduction. Cambridge University Press, Cambridge.
C. Kay and K. Allan. 2015. English Historical Semantics. Edinburgh University Press, Edinburgh.
M. Kytö, M. Rydén, and E. Smitterberg, editors. 2006. Nineteenth-century English: Stability and change. Cambridge University Press, Cambridge.
T. Mikolov, K. Chen, G. Corrado, and J. Dean. 2013. Efficient estimation of word representations in vector space.
R. Řehůřek and P. Sojka. 2010. Software Framework for Topic Modelling with Large Corpora. In Proceedings of the LREC 2010 Workshop on New Challenges for NLP Frameworks, 45–50, Valletta, Malta. ELRA.
P. H. Schönemann. 1966. A generalized solution of the orthogonal procrustes problem. Psychometrika, 31: 1–10.
R. Al-Ghezi and M. Kurimo. 2020. Graph-based Syntactic Word Embeddings. In Proceedings of the Graph-based Methods for Natural Language Processing (TextGraphs), pages 72–78, Barcelona, Spain (Online). Association for Computational Linguistics.
O. Levy and Y. Goldberg. 2014. Dependency-Based Word Embeddings. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers), pages 302–308, Baltimore, Maryland. Association for Computational Linguistics.
N. Pedrazzini and B. McGillivray. 2022. Machines in the media: semantic change in the lexicon of mechanization in 19th-century British newspapers. Proceedings of the 2nd International Workshop on Natural Language Processing for Digital Humanities, 85–95, Taipei, Taiwan. Association for Computational Linguistics.
Check out other projects